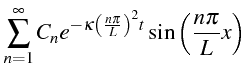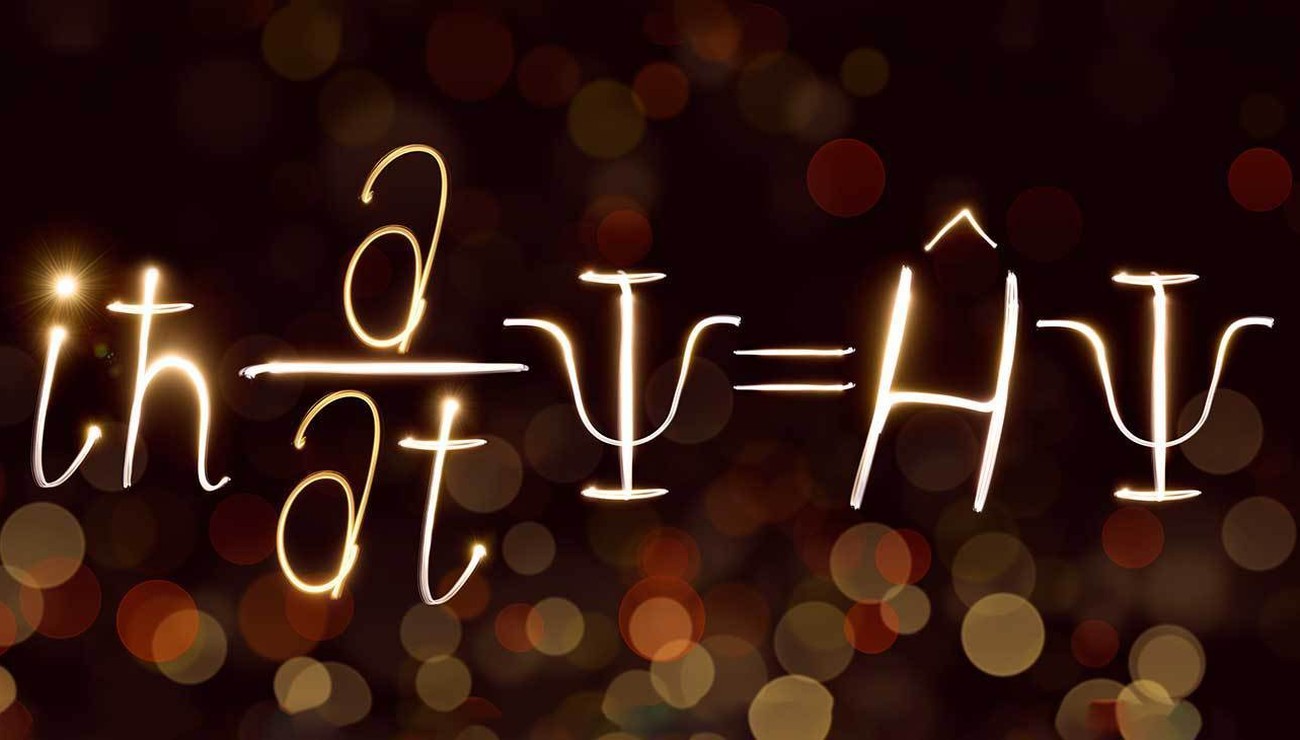MathematiKA

Cours de Mathématiques dans l'enseignement secondaire et les études supérieures
Les Mathématiques, à quoi ça sert ?
Les Mathématiques sont un outil, au même titre qu'un marteau et une enclume, mais celui-ci est purement abstrait. Il se développe en fonction de l'imagination, l'intuition
et la force de calcul de chacun. Les Mathématiques permettent de calculer, modéliser, anticiper, comparer, aider à la compréhension de notre monde (physique quantique), etc...
La liste est non exhaustive. Dans notre quotidien, les maths servent principalement à compter. Pourtant, "l'essence même des Mathématiques est la
perception des relations".
Quel lien existe-t-il entre le rayon d'un cercle et sa circonférence ? Y-a-t' il une relation entre le mouvement d'un solide et sa vitesse ?
Quelle équation régisse la propagation des ondes ? Etc...
Voici quelques exemples d'applications des Mathématiques.
a) Calcul de la hauteur d'un arbre.
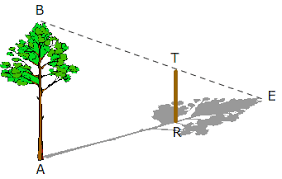
Imaginons qu'un botaniste plante un bâton TR de 1,6m de hauteur. Son ombre RE a une longueur de 2,5m et l'ombre AE de l'arbre mesure 20m. On modélise alors la situation
via le dessin ci-dessous (non à l'échelle) où l'arbre et le bâton sont parallèles.
Quelle est alors la hauteur AB de cet arbre ?
La réponse est 12,8 m grâce à l'application du théorème de Thalès !
b) Calcul d'un prix avec remise.
Mise en situation : "Martin veut profiter des soldes pour s'acheter un nouveau blouson. Il hésite entre deux modèles. Comme il n'arrive pas à choisir, il achète le moins
cher des deux. Quel blouson Martin choisit-il ? Quel est alors son prix ?"
Résolution : Pour comparer les deux prix, il faut d'abord calculer les prix après réduction de chaque article.
1er méthode. Pour le blouson marron à 69€ avec -15%, appliquons un produit en croix à l'aide de ce tableau de proportionnalité.
| Prix en euros (€)
| 69
| x
|
| Pourcentage %
| 100
| 15
|
69€ est le prix initial : il correspond au prix total, donc au pourcentage de 100%.
Dans la case de l'inconnu, x = 69 * 15 /100 = 10,35€ (produit en croix).
10,35€ est donc la réduction à effectuer au prix initial.
69€ - 10,35€ = 58,65€ est alors le prix soldé du blouson marron.
Calculons maintenant le prix après remise du blouson beige.
2e méthode. Il coûte 73€ avec -20%.
Le nouveau prix est donnée par : 73€ * (1-20/100) = 73€ * 0.8 = 58,4€, où (1 - 20/100) est le coefficient multiplicateur associé à la réduction de -20%.
Si Martin achète le moins cher des deux, il choisit alors le manteau beige.
c) Calcul d'un angle dans un triangle rectangle.
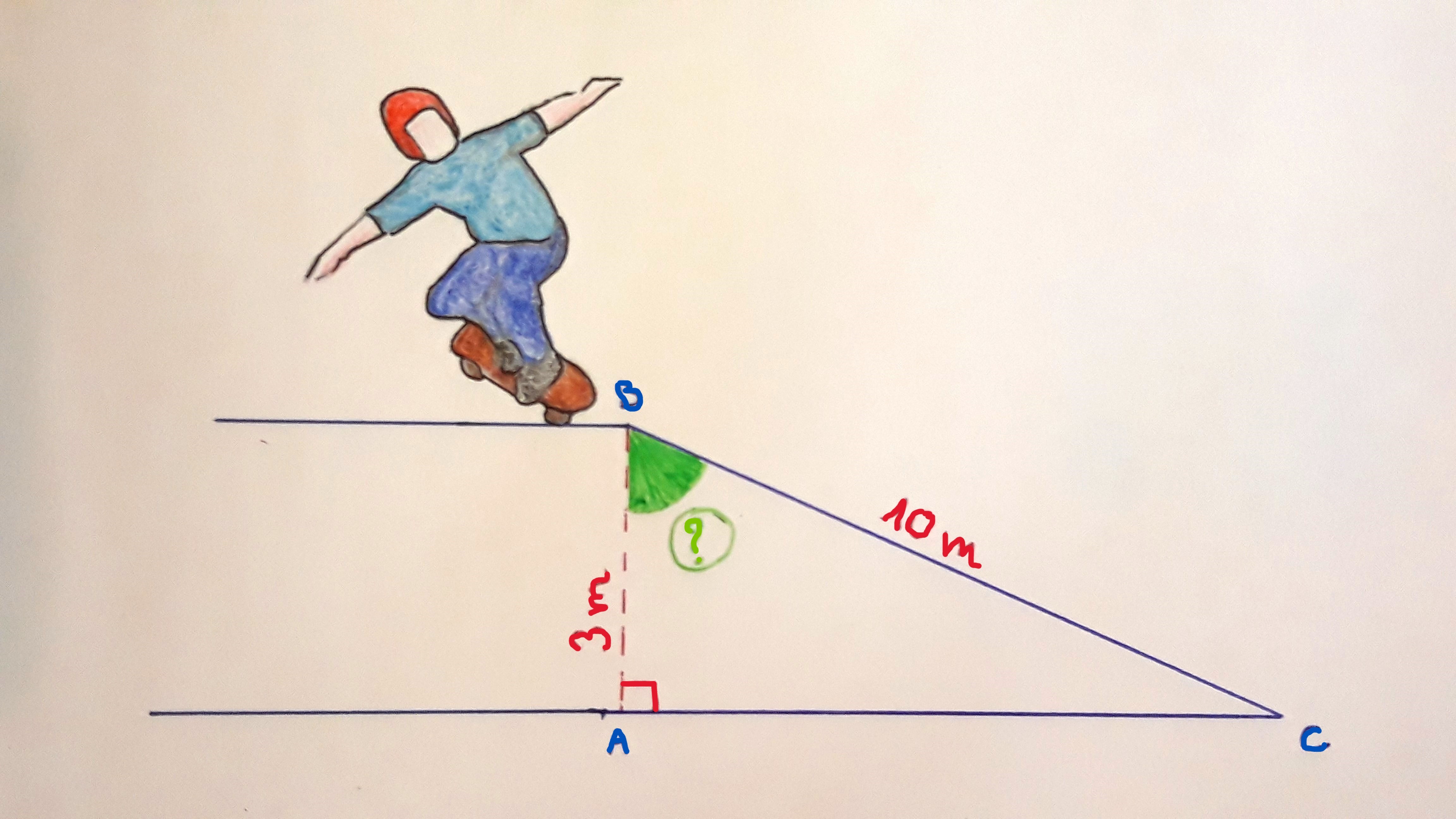
Exemple : "Voici la rampe de départ prévue par les organisateurs d'une compétition de skateboard. Pour être conforme au règlement, la mesure de l'angle ABC (avec un chapeau)
de cette rampe doit être comprise entre 70° et 75°. Cette rampe est-elle conforme ?"
Réponse : il faut un peu de TRIGONOMETRIE !
On modélise la rampe de skate par le triangle ABC rectangle en A : le côté BC est l'hypoténuse. D'après le schéma ci-dessus il mesure 10 m.
De plus, le côté AB qui mesure 3 m, est adjacent à l'angle ABC (avec un chapeau).
On utilise alors la formule du cosinus, ce qui nous donne :
cos (ABC) = AB/BC = 3/10.
Ainsi à la calculatrice (en mode degré !), l'angle ABC = arccos (3/10) ou bien cos^-1(3/10), soit environ 72,54° arrondi à 0,01 près.
Comme 75°> 72.54° > 70°, la rampe est donc bien conforme.
d) Calcul d'une surface à peindre.
Exercice incontournable au BREVET, le calcul de surface "complexe" à de réelles applications dans la vie. En voici un exemple :
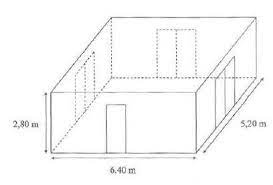
"Une entreprise doit rénover un local. Ce local a la forme d'un parallélépipède rectangle. La longueur est 6,40 m, et la largeur est 5,20 m et la hauteur sous plafond est
2,80 m. Il comporte une porte de 2 m de haut sur 0,80 m de large et trois baies vitrées de 2 m de haut sur 1,60 m de large.
Peinture des murs et du plafond :
Les murs et le plafond doit être peints.
L'étiquette suivante est collée sur les pots de la peinture choisie :
- Séchage rapide ;
- Contenance : 5L ;
- Utilisation recommandée : 1L pour 4 m².
De combien de pots de peinture l'entreprise doit-elle disposer pour ce chantier ?" Vous avez 15 minutes !!!
e) Résolution d'équations différentielles appliquées à la physique.
Exemple : étude des oscillations libres dans un circuit électrique de type (L,C), mise en équation du système, équation en charge.
Désignons à un instant t par q(t) la charge portée par le condensateur, par i(t) l'intensité du circuit et par uC(t) et uL(t) les tensions respectives aux bornes de C
et de L.
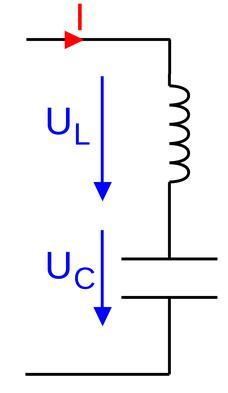
uL est la tension de la bobine,
uC est celle du condensateur.
|
Les conditions initiales sont les suivantes : le condensateur est chargé de telle façon que q(t = 0) = qo > 0 soit la charge de l'armature positive (rappelons que qo = C*uC(t = 0),
où C est la capacité du condensateur en farad (F) ; l'interrupteur étant ouvert, l'intensité initiale est nulle i(t = 0) = 0. À l'instant initial le circuit est fermé.
En choisissant les tensions et l'intensité instantanées comme indiqué sur le schéma et en exprimant la loi d'Ohm aux bornes des dipôles L et C, (compte tenu des conventions
de signes des circuits électriques), il vient :
uL(t) + uC(t) = 0. (*)
Or on sait que dans un condensateur, la quantité de charge q(t) vérifie : q(t) = C*uC(t), donc on a uC(t) = (1/C)*q(t).
De plus, uL(t) = L*(di/dt), c'est la tension aux bornes d'une bobine sans résistance, et comme i(t) = dq/dt, en dérivant, on obtient l'égalité : di/dt = d²q/dt²,
d'où uL(t) = L*(d²q(t)/dt²).
Ainsi en remplaçant les expressions de uL et uC dans l'équation (*) on a :
L*(d²q(t)/dt²) + 1/C*q(t) = 0,
soit (d²q(t)/dt²) + 1/LC*q(t) = 0.
Cette équation différentielle d'ordre deux est du type harmonique, de pulsation propre wo = (1/LC)^(1/2) et de solution générale q(t) = qm*cos(wo*t + P), avec P un réel représentant
la phase à l'origine des dates en radians (rad). Compte tenu des conditions initiales, la solution finale s'écrit q(t) = qo*cos(wo*t).
La charge q(t) oscille donc entre les valeurs qo et -qo, autrement dit le condensateur se décharge et se charge alternativement, d'où le nom de circuit oscillant
(remarquons qu'il n'y a pas de résistance dans le circuit, donc il n'y a pas d'amortissement, idéalement).
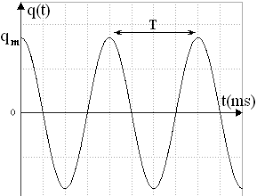
courbe représentant la quantité de charge en fonction du temps.
|
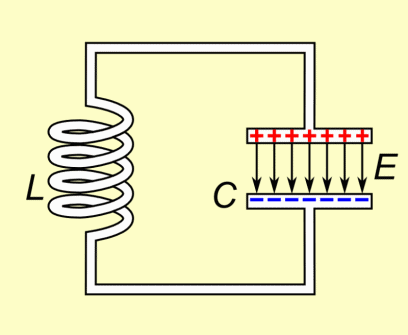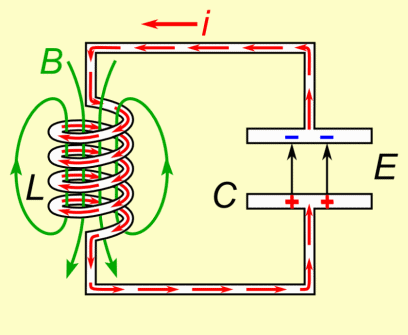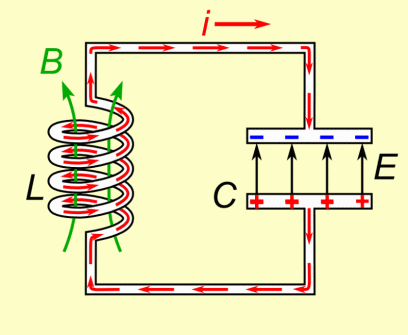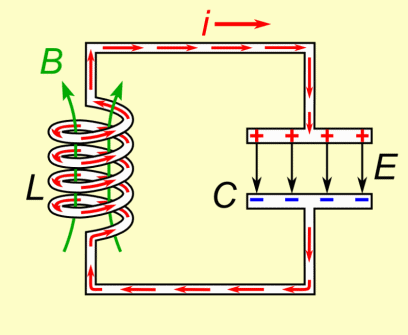
Le condensateur se charge et se décharge alternativement.
|
f) La théorie des séries de Fourier.
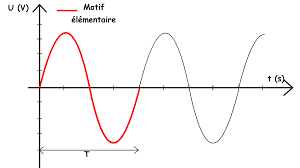
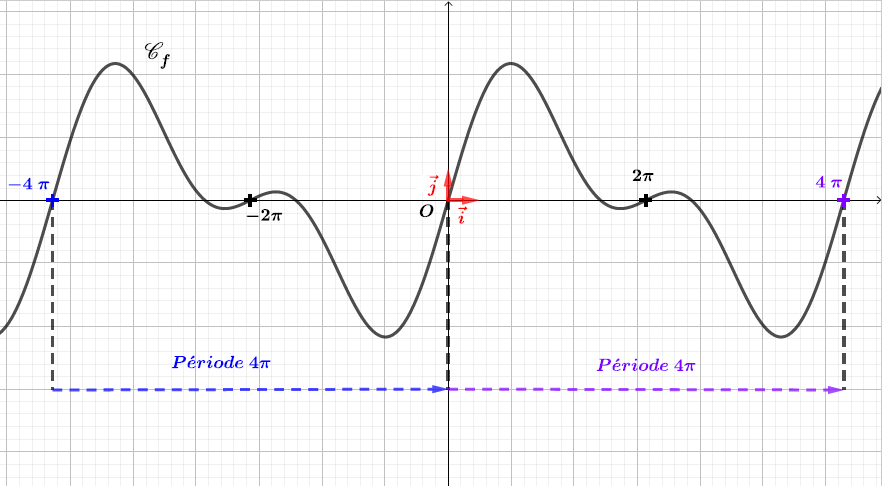
En analyse harmonique, les séries de Fourier sont un outil fondamental dans l'étude des fonctions périodiques, c'est-à-dire des fonctions dont la courbe représentative
est caractérisée par un motif répétitif à intervalle régulier, de période T (voir schéma ci-dessous).
L'idée est de décomposer un signal périodique (ex: courant électrique, ondes cérébrales, ondes sonores, etc...) en un somme de sinusoïdes, à savoir des fonctions de types
f:x-> a*cos(ax) ou g:x->b*sin(bx), ou a et b sont des nombres réels.
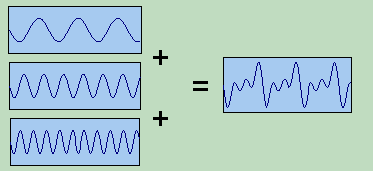
La somme des trois fonctions sinusoïdales de gauche donne le signal de droite.
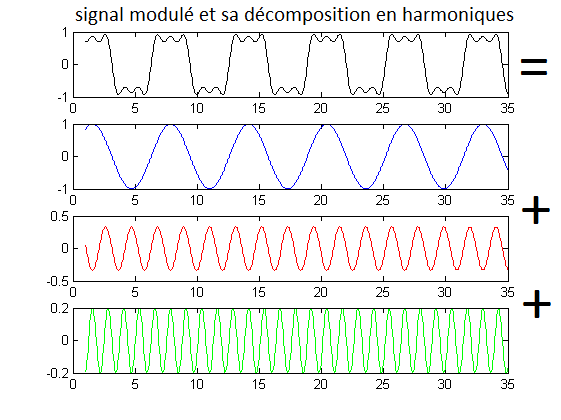
De même, le signal en créneau de l'image d'à côté se décompose suivant les trois fonctions sinusoïdales bleue, rouge et verte.
|
|
L'étude d'une fonction périodique par les séries de Fourier comprend deux volets :
- l'analyse, qui consiste en la détermination de la suite de ses coefficients de Fourier.
- la synthèse, qui permet de retrouver la fonction à l'aide de ces coefficients.
Il y a donc une correspondance entre la fonction périodique étudiée et ses coefficients de Fourier. Toutes les opérations telles que la somme, la dérivation ou la recherche
de primitive passe par cette analyse plus simple à manipuler. Autre exemple, grâce à l'analyse harmonique, on connaît pour x entre 0 et L donné et t > 0, u(x,t) la fonction
solution de l'équation de la chaleur égale à la série :
g) Les ondes se propagent selon... l'équation de Schrödinger !
"L'équation de Schrödinger, conçue par le physicien autrichien Erwin Schrödinger en 1925, est une équation fondamentale en mécanique quantique.
Elle décrit l'évolution dans le temps d'une particule massive non relativiste, et remplit ainsi le même rôle que la relation fondamentale de la
dynamique en mécanique classique."
Retour à la page d'accueil.